| �⡡�� | |
|---|---|
| ̾������ | ���� |
| �����ֹ� | ���ͻ� |
| �ꡡ��̾ | Ǥ�դ�̵�����κ��ˡ |
| ������ | �������� WEB���̵�����Τ��Ȥ����Ƥ��ޤ����Ȥ�����HP�˹Ԥ������ꡢ��������𤦼���Ǥ��� �����Ƕ��̤Ǥ�������ǽ���ϰϤǤ���������������ʸ���ϽпȤǿ��ؤ�����Ū�˳ؤ�����Ȥ�����ޤ��� Ǥ�դ�̵�����κ�ޤ���ˡ�˴ؤ��ƻǤ��ޤ��� ̵������ȯ�����ǥ���Ȥβ��ϴ����ؤ��礭������̤����Ƥ���Ȼפ��ޤ��� ����Ǥ�դ�̵������Ⱦ�ߤ�ľ�¤˱�������������������ˤ�����Ǥ��줿ľ�¤���¦��ñ�̤Ȥ��Ƥ���ȿ��¦��ľ�¤������ܤˤ���Ȥ��ο��������ޤΤ褦��̵�����Ȥʤ�ޤ���1:a����Ǥ�դ������ܤˤ��뤳�Ȥˤ��Ǥ�դο���̵���������뤳�Ȥ��Ǥ��ޤ��� ����������ˡ�Ȥ��̤˺ǽ�ˡ�1:a����1:1���ˤȤ�缡a�������ܤ��礭������Ⱦ�ߤ�缡�礭�����뤳�Ȥˤ�äƤ�Ǥ�դο���̵���������뤳�Ȥ��Ǥ��ޤ����� ����������ξ��������ϻ��ѷ����ߤ����ܤ���Ȥ������Ȥ˰�¸����Ȥ������ȤǤ��� 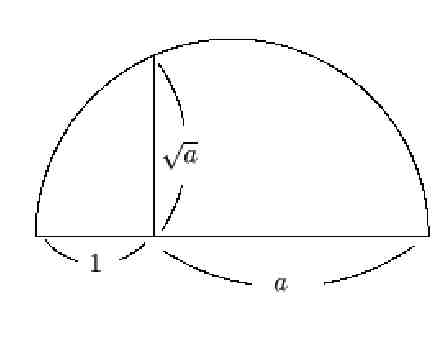 ����������ʸ�Ϥϥץ�ȥ�Ρإ�Υ��87a�ʲ��������Ǥ�������ʸ�Ϥ�Ǥ�դ�̵�����κ�ޤζ�����Ȥ��Ʋ���ǽ���ݤ��������Ǥ����������Ǥ��� for example, [87a] whether a certain area is capable of being inscribed as a triangular space in a given circle: they reply--I cannot yet tell whether it has that capability; but I think, if I may put it so, that I have a certain helpful hypothesis for the problem, and it is as follows: If this area2 is such that when you apply it to the given line3 of the circle you find it falls short4 by a space similar to that which you have just applied, then I take it you have one consequence, and if it is impossible for it to fall so, then some other. Accordingly I wish to put a hypothesis, before I state our conclusion as regards inscribing this figure in the circle by saying whether it is impossible or not. 5.����������ǽ���ݤ��Ϥ٤ĤȤ��ơ��嵭���������뤤�ϣ�������ˡ������ط�������������ˡ������Ǥ��礦�����ĤޤꡢǤ�դ�̵����������ˡ������Ϣ�椢�뤤�ϵ���Ȥ���ɽ�����뤤�����뤳�Ȥϲ�ǽ�Ǥ��礦�������ꥷ����̵������ȯ������Ƥ������Ȥ��Τ��Ƥ��ޤ��������κ����ˡ������˴�����Ū���̤����Ū���̤Ȥ��Ƽ�갷����ˡ��ͤ��Ф��Ƥ����������ǽ��������Ȥ��������Ǥ��� �����Ƕ��̤Ǥ�����������ĺ���������ͭ����¸���ޤ� |
| ü���ɣ� | ����ϥ����褿��Τ���ƼԤε��Ĥ�����ž�� |
| �������� | Sep 05 2004 |
| ���ֻ� |
���礵��� �ʲ��Τ�����,�ͤ�HP����Υȥ���ݥ��ȤηǼ��ĤˤǤ褱��С����������Ƥ��������ޤ�. ̵�����Ȥ�����Τ��Ф�������,����Ū���������ʤ�,�����������Ƥ��������ޤ�. ���Τ��ֻ�������С��ݥ��Ȥ����˽��Ȥˤ��ޤ��礦�� �����ŵ��Ū�ʸ�����ˤʤäƤ��ޤ�. ��Ϥꡤ�������٤Ͽ��ؤΤ����Ȥ����ؽ���ʤ��äƤ���������褤�Ȼפ��ޤ�. ��ǯ��,���ܿ��ض���Ȥ�����Τ���ޤ���. ���ؤ����ܤ�����ۤɿ����ʤ��Ƥ⡤���ؤ��������Ȥ��������ǡ����ؤˤĤ��� �����ä���ä���,�����Ǥ����Ǥ��� ��̣����äƤ���������褦�ʤ�,�������Ʋ�����. ����ˤϡ������HP�ιⵡǽ�ʷǼ��Ĥǡ��ä����ä���, ������ꤹ�뤳�Ȥ��Ǥ��ޤ��� �ޤ����ͤ�HP��������Ƥ���ޤ��Τǡ����ܿ��ض����HP������������. |