MyBookのホーム
『解析教程』.『微分トポロジー講義』.
『数理解析のパイオニアたち』.
『数学名所案内』.
『数論の3つの真珠』.
『代数学とは何か』.
『黄金分割』.
『天書の証明』.
『数学の最先端 21世紀への挑戦3』
『シンメトリー』
『微分のはなし』
『古典群:不変式と表現』
『直線と曲線 ハンディブック』
『数学者列伝』
『面積・体積・トポロジー』
『微分のはなし』
『積分と微分のはなし』
『文明開化の数学と物理』
『代数入門』
『微分の基礎 これでわかった!』『微分の応用 これでわかった!』『本格数学練習帳』
『確率で読み解く日常の不思議』『数学の作法』『幾何教程』『孫サイ数』
『実解析の助け舟』

数学用語の定義・説明

人名索引総目次
トップへ
 う
う 
ヴァンデルモンドの行列式
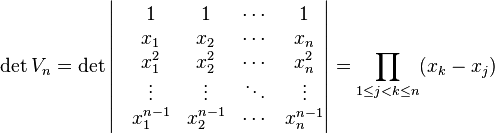
ファンデルモンドの行列式と書かれることも多い.答が差積であるために重要であり,この行列式の計算ができることが,行列式の計算の習熟に対する目安になるので有名な行列式である.
行列式の元の行列をヴァンデルモンドの行列というが,多項式近似の一般解法に使われるが,いつでも簡単に行くわけではない.
トップへ
 お
お 
オイラーの公式
(1) eiπ=-1 (i=√-1)
(2) exp(iθ) = cos θ+ i sin θ
(3) 多面体の頂点の数をV,稜の数をE,面の数をSをするとき,V-E+S=2 となる.オイラーの多面体定理とも言う.
(4) π/4 = arctan (1/2) + arctan(1/3) , π/4 = 5 arctan (1/7) + 2arctan(3/79)
トップへ
 け
け 
ケーニヒスベルクの橋
オイラーは,当時ケーニヒスベルクの町に掛かっていた7つの橋を,すべて,同じ橋を一度しか渡らないようにして渡れるか,という問題を解いた(1673年頃).
グラフとして一筆描きができるかという問題に直して解答し,グラフ理論のひいてはトポロジーの嚆矢となった.
その橋の配置図が多くの本に描かれているが,かなりまちまちで(向きさえ一定していない),何が正しいのかわからない状態が続いていた.ケーニヒスベルクは中世からかなり発達した町であり,レギオモンタヌス以来多くの学者が輩出し,研究生活を送った場でもある.しかし,第2次大戦後ソ連に接収され,現在もロシアの領地である.軍港としての役割も大きく長い間外国人には近づくことができない場所であった.
日本では地図を得ることができない.
幸いに,安野光雅氏の算数絵本『はじめてであうすうがくの絵本 3』には,ケーニヒスベルクの古地図が掲載されていて,実際の橋の配置についての知識は得られる.
しかし,橋の名前についての情報はどこにも得られなかった.それが実は『数学名所案内 下』の第19節図19.1(98ページ)に載っている.
管理者が訳したものなので,最初にこれを知った日本人ということになる.
少し裏話をしよう.もちろん英語の本なので,橋の名前は英語に翻訳ないし音訳されていた.それをあげると.
Shopkeepers Bridge , Blacksmith Bridge ,
Wooden Bridge ,
Honey Bridge ,
High Bridge ,
``Guts''Giblets Bridge ,
Green Bridge
であった.最初はこれを日本語に訳して,
商人橋,鍛冶屋橋,材木橋,蜂蜜橋,高い橋,臓物橋,緑橋
とするつもりであった.しかし,いかにも「臓物橋」というのはすごい名前である.
橋のたもとに食肉解体場でもあって,普通の人があまり通行しないような地域だったのだろうか.
英語名でも,これ1つ浮いている.何とか,当時の橋の名前が分からないだろうか.東京に行くたび地図屋を覗いて廻るとか,普通に考えられる手段を取ってみたが,国内では分かりそうもなかった.しかし,ソ連に占領される前はドイツ文化圏の町であった訳だし,翻訳を出版する出版社の本社がドイツにあることから,問い合わせてもらった.当時のドイツ語の橋の名前が
Kr\"amer Br., Schmiede Br., Holz Br., Honig Br. , Hohe Br., K\"ottel Br., Gr\"une Br.
であったことが分かった(もちろん \"は次の字母に冠するウムラウトを意味).これなら,
商人橋,鍛冶屋橋,材木橋,蜂蜜橋,高い橋,小児橋,緑橋
となる.恐らくは,K\"ottel Br. を Kuttel Br. と読み間違ったのではないかと,編集者との間では了解が成立した.が,出版間際のころ,著者と連絡が取れなかった.実はその数週間前に,広島大学で行われた日本数学会の秋季総合分科会に,著者が特別講演をする予定になっていたが,体調を崩して帰国したばかりのときだった.そこでやむなく,ドイツ語の橋の名前を音訳した.
クレーマー橋, シュミーデ橋, ホルツ橋, ホーニヒ橋,
ホーエ橋, ケッテル橋, グリューネ橋
を,掲載することにした.いまなら,
あきない橋,鍛冶屋橋,材木橋,蜂蜜橋,高橋,おさなご橋(または子橋),緑橋
とでもしただろうか.
トップへ
 こ
こ 
合同数
a2+b2 = c2 を満たす正の有理数の3つ組 (a, b, c) に対して,ab/2が整数なるとき,ab/2を合同数と言う.
(有理数辺の直角三角形の面積になり得る整数のこと.)
『数学名所案内 上』の附録Eに説明しておいたので,参照されたい.
ちなみに,1から100までの合同数は,
5, 6, 7, 13, 14, 15, 20, 21, 22, 23,
24, 28, 29, 30, 31, 34, 37, 38, 39, 41,
45, 46, 47, 52, 53, 54, 55, 56, 60, 61,
62, 63, 65, 69, 70, 71, 77, 78, 79, 80,
84, 85, 86, 87, 88, 92, 93, 94, 95, 96
の50個だけであることが知られている.
これは元々,フィボナッチが,パレルモのジョヴァンニから,「 x2+5 と x2-5 が同時に平方数であるような x を求めよ」という問題を出されたことに始まっている.これを一般化して「 x2+C と x2-C が同時に平方数であるような x を求めよ」という問題に解があるような数 C を congruum と呼んだ.これが合同数 congruence number の定義と同値であることが容易に示される.
フィボナッチはまた,x2+y2とx2-y2が同時に平方数にはなり得ないことを示しているが,そのことは 1 が合同数でないことと同値である.
トップへ
 さ
さ 
三角形の中心
三角形の中心と呼んでよいものには,古典的な五心,つまり,重心,内心,外心,垂心,傍心(ただしこれは3点ある)がある.
それ以外にも,ジェルゴンヌ点,九点円の中心,フェルマ点,トリチェリ点,ナゲル点(ジェルゴンヌ点の等長共役点isotomic conjugate),ブロカール点,ド・ロンシャン点(外心に対して垂心と対称な点),
ナポレオン点,ソディ点,対中点(symmedian point,ラモアン点,グレーべ点ともいう,重心の等角共役点isogonal conjugate),フォイエルバッハ点などがある.
トップへ
 し
し 
シュルツの公式
π/4 = arctan (1/2) + arctan(1/5) + arctan(1/8)
ダーゼはこの公式により(1706年), πを205桁計算した.
トップへ
トップへ
 す
す
ストラングの奇妙な図形
sin n (n:整数)の値を,nの軸を対数目盛りにしてプロットすると,浮かび上がってくる網目模様のこと.『解析教程 上』第I章§4図4.6(p.59)参照.
トップへ
トップへ
 そ
そ 
素数いろいろ
素数概念は1つしかないが,類似というか近似というか,概素数,擬素数,半素数,殆素数のようなものと,
メルセンヌ素数などのようなある種の数の中で素数であるもののようなものがある.
擬素数(pseudoprime)とは様々な素数判定テストを通過する合成数のことで,フェルマテストを通過するのをフェルマ擬素数,オイラーテストを通過するのをオイラー擬素数と言う.
他にも,フロベニウス擬素数,オイラー・ヤコビ擬素数,リュカ数擬素数,フィボナッチ擬素数,ペラン擬素数,カタラン擬素数,強擬素数,強リュカ擬素数などがある,
メルセンヌ素数: 2n - 1 (n = 2, 3, 5, 7, ...)の形の素数
フェルマー素数: Fn=22n + 1の形の素数
階乗素数 n! ± 1 の形の素数
素数階乗素数 p1p2・・・pn ± 1 の形の素数(ここでpiはi番目の素数)
トップへ
 た
た 
高野喜久雄の公式(1982)
π/4 = 12 arctan (1/49) + 32 arctan (1/57) - 5 arctan(1/239) + 12 arctan(1/110443)
金田康正が日立のスーパーコンピュータを用いてπを1兆2411億桁計算した時(2005年)に使った公式.マチンの公式の改良版.類似なものに同じ1982年に発見された柴田昭彦の公式
π/4 = 17 arctan (1/22) + 3 arctan (1/172) - 2 arctan(1/682) -7 arctan(1/5357)
がある.
単位分数(unit fraction)
自然数nを分母として,分子が1である形をした分数のこと.
古代エジプトの数学教科書にあることで有名.アーメスの書(リンドパピルス)には2/nを単位分数の和に表わす方法を結果が書かれている.ただし,「分解するときの単位分数の分母は異なること」という条件が付いている.
同じやり方をすれば個々の場合に,任意の分数を整数と異なる分母の単位分数の和に書くことができることがわかる.ただし,証明はフィボナッチが1202年に行うまではされなかった.
そういう意味でフィボナッチの定理と呼んでもいいのだが,事実は数千年前から知られており,さらに,この種の主張に証明をするという意識がなかったこともあって,そう呼ばれることは少ない.
真分数を単位分数の和で表わすことができるのはよいのだが,いくつでもよいというのは少し歯切れが悪い.条件を付けて3つ以下にできないかと考えた人たちがいる.
エルデシュ・シュトラウスの予想(1948):n≧2のとき,4/nを3つ以下の単位分数の和に書くことができる.
シェルピンスキの予想:n≧2のとき,5/nを3つ以下の単位分数の和に書くことができる.
これらの場合,分母が異なるという条件は付いていないが,まだ証明はされていない.もちろん,かなり大きな数以下では成り立つことが証明されており,またコンピュータを使ってその数は相当大きくできている.
チュドノフスキーの公式(1987)
1/π = 12 Σk=0∞ (-1)k(6k)!(13591409+545410134k) / (3k)! (k!)36403203k+3/2
チュドノフスキー兄弟が金田康正とπの計算の世界記録を争ったときに使った公式.
トップへ
 は
は 
バシェ方程式
整数 a に対して y2-x3 = a という形をした方程式のこと.
1909年に,トゥエが,これには有限個の整数解しかないことを示した.ちなみに a=7 に対しては解がなく,その証明はたとえば『数学名所案内』の第3節にある.
トップへ
 ひ
ひ 
ピュタゴラス数
直角三角形の3辺になり得る正の整数の3つ組 (a, b, c) をピュタゴラス数またはピュタゴラス3つ組と言う.(a2+b2 = c2 をみたす正の整数の3つ組 (a, b, c)のこと).
これは無限個,しかも3パラメータを含んでいる.一般に,k, u, v (u>v) を正の整数とするとき,
a=k(u2-v2), b=2kuv, c=k(u2+v2)
はピュタゴラス数になる.証明の書いてある日本語の本は多く存在しているが,できれば自分で考えてみよう.
トップへ
 ふ
ふ 
双子素数定数
N以下の素数の個数が,素数定理と類似に,漸近的に
2C2N / (log N)2となるという予想を双子素数予想と言い,この定数 C2N を双子素数定数という.予想が成り立つかどうかは知られていないが,この定数の評価はレンチJr.によって得られている.
トップへ
 へ
へ 
ベイリー・ボールウェイン・プラウフの公式
BBP公式
π=∑k=0∞ 1/16k (4/(8k+1) -2/(8k+4) -1/(8k+5)-1/(8k+6))
これにより,πの2進法表示(8進法でもよい)の好きな桁だけを計算することが可能になる.これは1995年に
ベイリーとP.ボールウェインとプラウフにより発見された。
トップへ
 ま
ま 
マチンの公式
π/4 = 4 arctan (1/5) - arctan(1/239)
ジョン・マチンはこの公式を発見し(1706年), arctan の展開を利用して,πを100桁計算した.詳しくは『解析教程 上』第I章第4節を参照.この公式は,20世紀になって,コンピュータによる計算が始まるまでの計算公式の基礎になった.
メルセンヌ素数
素数であるメスセンヌ数 Mp=2p-1 のこと.
2011年現在47個のメルセンヌ素数が確認.40番目までは番号も確定.
トップへ
 り
り 
リーマンの関数
級数で定義される関数
f(x)=Σn=1∞ sin (n2x)/n2
= sin x + sin (4x)/4 + \sin (9x)/9 + ・・・・・・
のことで,一様収束するので連続であるが,リーマンはどこでも微分可能であると考えたが,ワイエルシュトラスは自分は証明できないと表明する.後に,1970年になって,ジャーヴァが x=πで微分可能であることを示す.
トップへ
 る
る 
ルーカス・レーマー・テスト
メルセンヌ数 Mp=2p-1 が素数であることと,Mpが
Spの約数であることは同値である.
ここで,数列 Sp は帰納的に, S2=4, Sn=Sn-12-2 として定義されたもの.
トップに戻る。
人名索引の中で触れた数学用語・術語を挙げて行く予定である.
リクエストがあれば応じるので,kanielabo@gmail.com(@を@に直してお使いください)へメールして下さい.




 う
う 

 お
お 
 け
け 
 こ
こ 
 さ
さ 
 し
し 
 す
す
 そ
そ 
 た
た 
 は
は 
 ひ
ひ 
 ふ
ふ 
 へ
へ 
 ま
ま 
 り
り 
 る
る 